


Therefore, Standard Error in mean will be 2.42.
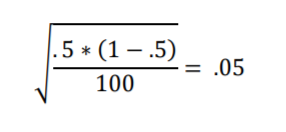
The following are the popular measures for data collection.Ģ) Standard Error in the Sample Proportion:ģ) Standard Error in the Difference between means: The Formula for Standard Errorĭepending upon the statistical measure in the corresponding data, relevant methods will be used to measure the standard error. We might be required to find standard errors for other statistical measures also. When we are asked to find the sampling error, you’re probably finding the standard error. Confidence Level Z Value 90: 1.645: 95: 1.960: 98: 2.326: 99: 2.576: How do you find the t value for a 95 confidence interval The t value for 95 confidence with df 9 is t 2.262. For example, the calculation is different for the mean value or proportion value. Calculating a confidence interval involves determining the sample mean, X, and the population standard deviation,, if possible.Z-values for Confidence Intervals. How we find the standard error depends on what statistical measure we need. While the standard error uses sample data, standard deviation uses population data. Although the two terms are essentially equal, there is one important difference. standard error: the standard deviation of the distribution of the sample proportion Confidence Interval Estimates for the Population Proportion Case 1: You are given the confidence level you desire (90 confidence interval) 1.Assign the percent to D (in decimal form) 2.Find: value D + (1 D) / 2 3.If on calculator: INVNORM(value) If using tables: Look up value in the middle 2. The higher the number, the more spread out our data is. SE is very similar to standard deviation. A small standard error would mean that the population is in a uniform shape. A large standard error will indicate that there is a lot of variability in the population. Standard Error is telling how well the sample mean estimates the true population means. In order to determine how well the sample is representing the population, we need to go out and measure the standard error in the specific measurements. Many computations are required for this collection. To use it, enter the observed proportion, sample size, and alpha (half of the desired confidence level so. There are many ways to define a population, and we always need to be very clear about what is the population. This confidence interval calculator is designed for sampling population proportions. A population is an entire group from which we take the sample. In the theory of statistics & probability, the below formulas are the mathematical representation to estimate the standard error (SE) of sample mean (x), sample proportion (p), difference between two sample means (x 1 - x 2) & difference between two sample proportions (p 1 - p 2 ). The standard deviation (often SD) is a measure of variability. 1 The contrast between these two terms reflects the important distinction between data description and inference, one that all researchers should appreciate. Use the given information to calculate the sample proportion,, and the standard error of the proportion, SEP, for the described sample population. For example, the sample may be the data we collected on the height of players on the school’s team. The terms standard error and standard deviation are often confused. In statistics, the word sample refers to the specific group of data that is collected. The highly accurate margin of error calculator helps to find margin of error of a survey by taking sample size, proportion percentage, population size & confidence level. Let us learn the concept! Standard Error Formula What is the standard error? In this article, we will discuss the standard error formula in various cases. The sample mean deviates from the population and that deviation is known as standard error formula. The accuracy of a sample that represents a population is known through this formula. These are the familiar formulas, showing that the calculation for weighted data is a direct generalization of them.The standard error is an important statistical measure and it is related to the standard deviation. Since the $X_i$ are independent and each one has variance $\text$. In a simple random sample $X_1, \ldots, X_n$ where each $X_i$ independently has a Bernoulli$(p)$ distribution and weight $\omega_i$, the weighted sample proportion is Standardize the (positive) weights $\omega_i$ so they sum to unity. \begingroup Even more precisely, 'standard error' of the proportion refers to the standard deviation of the distribution of the sample proportions from random samples of the particular sample size from the population of interest. Yes, this formula generalizes in a natural way.


 0 kommentar(er)
0 kommentar(er)
